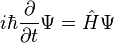Collision

Collision is an important fact in Natural life. In this article we are going to discuss the collision between Natural bodies in physical science major.

Let, 2 point objects say O₁, O₂ with mass m₁, m₂ respectively collide with initial velocity u₁,u₂ and final velocity v₁,v₂ with Coefficient of restitution α = (v₁ - v₂ ) / (u₂- u₁), the ratio of final and initial relative velocities.

Now we will have following 2 equations in hand :-
1.  α = (v₁ - v₂ ) / (u₂- u₁)
2.  m₁v₁ + m₂v₂ = m₁u₁  + m₂u₂ , The Conservation of Moments.

Now solving them we get

v₂  = v₀  + μ₂. α. ( u₂ - u₁)
v₁  = v₀  + μ₁. α. ( u₁ - u₂)

Where
v₀ = ( m₁u₁ + m₂u₂ ) / ( m₁ + m₂) , The velocity of the cm of the system.
μ₂ =   m₂ / ( m₁ + m₂) , Mass partition.

Now, if :-
1)  α = 0 then v₁ =  v_{2 ,}Totally inelastic collision.
2)  α = 1 then v₁ +  u₁  =  v₂ + u_2 ,Totally elastic collision.
3) Else, α ∈ (0,1) Natural Collision. :)

In only Natural and Inelastic collision Kinatic energy will be changed into other energy ( Heat , Internal energy etc ) For amount of mechanical energy loss just calculate

Q = 1/2 ( m₁v₁² + m₂v₂² - m₁u₁² - m₂u₂² )

Markov Chain

Many time we face some problem which can be formulated as a set S = {s_i} of state and a the probability to go from one state to another is given . A subset of that kind of problem is Markov chain .

Def(Markov Chain) :- A process organised on a set of states S = {s_i} where inter state transitional probability only depends on previous and next state i and j. So we can create a Transitional matrix P = {p_ij} consist of conditional probability to go from state j to i.  

We can also say that Pⁿ  is representing the matrix {pⁿij} where pⁿij is the probability to go state i from j in n steps.

Similarly we can say that Lt (n→∞) Pⁿ  = ∏ . 

The Outcome of Maxwell's Equations

The outcome is the establishment of electromagnetic wave and later it has been proved that Light is an EM wave.
Now we get E(x,t) = E(x - ct) . It is a function of  x,t. As natural continuous functions are Fourier transformable so can find Fourier transform of this wave w.r.t time and space.

E(x,t) = E(x) ∫f(w) e^iwt dw

Now if we assume that only one frequency 'n' is there so we get  :-
E(x,t) = E_s(x) e^2iπnt ~ E_s(x) cos(2πnt) [In real domain]

So, we get a frequency relation.

Now we want to determine the frequency velocity relationship.

We can further write that E(x,t) = Σ E₀ cos(2π(x/λ - n.t)) by taking Fourier transform about both x,t .

Now for a specific bi-periodic wave E(x,t) = E₀ cos(2π(x/λ - n.t)) we get that c = nλ .

Maxwell's Equations

From the experimental results on the search of Electromagnetism Maxwell had ultimately been able to create 4 golden rules of Electromagnetism.
They are :-

(i) ∇.E = ρ/ϵ 

(ii) ∇.B = 0 

(iii) ∇×E = -∂B/ ∂t 

(iv) ∇×B = μ(J + ϵ.∂E/ ∂t) 

E and B are electric and magnetic fields respectively at a point and ϵ,μ are electric and magnetic permittivity respectively. J is the electric current density. 

Notice that there is no mention of the reference frame in the above equations because these are true for any inertial reference frame. 

Now in free space J = 0 and ρ = 0 . So 

∇×B = μ₀ϵ₀.∂E/ ∂t  

=> ∇×∇×E = -  μ₀ϵ₀.∂²E/ ∂²t 

=> ∇(∇.E) - ∇²E   = - (1/c²) ∂²E/ ∂²t  

=> ∇²E - (1/c²) ∂²E/ ∂²t = 0 [ As ρ = 0 so from (i) ∇.E = 0 ]

=>( ∇² - 1/c² . ∂²/ ∂²t ) E = 0 

Similarly we can get ( ∇² - 1/c² . ∂²/ ∂²t ) B = 0 

For plane wave along +ve x axis E(x,t) = f(x - ct).

Friction and Viscocity

Friction is force acted on the boundary surface a body when it want to get a relative velocity w.r.t another body contacted by that boundary surface.

Friction F =  μN where N is the Normal Reaction.

Similarly for fluid the viscosity is  applied on a surface of the fluid by another surface.

Classical Mechanics

The mechanics of bodies fur larger than the Hydrogen atom and moving in the velocity fur less than the velocity of light in free space is called Classical Mechanics.

Key Scientists :-
1) Galileo Galilei 
2) Sir Isaac Newton
3) Johannes Kepler
4) Lagrange 
5) Bernoulli 


In this branch mass,velocity,force,energy,power,angular mechanics etc are discussed with the Analytical Mechanics with Generalized coordinates .

This mechanics originated from theories gained simple experiments and from there only mathematical search.

Quantum Mechanics

Quantum mechanics is a branch of physics which deals with physical phenomena at microscopic scales, where the action is on the order of the Planck constant. 

Action : It is defined in the classical physics by time integration Lagrangian L = (T - V) of a system.
           
where T is the kinetic-energy and V is potential energy of the system.

Most commonly, the term is used for a functional S which takes a function of time and (for fields) space as input and returns a scalar. 

                          

I think the wikipedia  is really a good document to have an initial understanding of Classical mechanics and variation calculus. 

Key factors of the Quantum mechanics :-

1) Wave-particle duality :- According to De Broglie hypothesis  Every wave is a particle and vice-verse.

where h is Planck's constant, E and p are Energy and momentum respectively. More λ is the wavelength and f is the frequency. 

2) Light is an accumulation of particle named photon :- Light is a wave and particle according to the De-Broglie hypothesis, the particles of light is called photon. 

The nature can be described as the particle interaction as well as the Wave superposition.

This is a nice video of Quantum Object Nature . :)

http://upload.wikimedia.org/wikipedia/commons/e/e4/Wave-particle_duality.ogv

3) Wave Mechanics :- The behavior of wave particle is been discussed in the wave mechanics. 

Schrödinger Equations paved the root of this mechanics. 

             or,

  

Heisenberg Uncertainty Principle

Heisenberg principle :- Heisenberg proved existence  of pair of properties say x and p(x) s.t 
                                     σ(x)σ(p(x))  ≥ h/4π  always.
This take us to a fact that such pair of properties both cannot be determined with absolute certainty.
For example :- 
Let, x is the position of a point particle and p(x) is its momentum at point x. 
The Heisenberg told that both x and p(x) can't be determine with absolute certainty (as standard deviation σ represents the amount of error / shift from certainty / uncertainty ).

What is the main cause behind this kind of behavior. The proof could be gained from the Heisenberg Microscope experiment .

For the detail prove see http://spiff.rit.edu/classes/phys314/lectures/heis/heis.html and
http://www.aip.org/history/heisenberg/p08b.htm .

The Heisenberg Principal paved the base of the Wave Mechanics .

Physics

Physics is a study of nature. The physical science view the nature as a dead or mechanical [ Strongly ruled by measuring mathematics ] object/collection of objects.

Every thing in the Nature is just a mechanism and the Nature is a huge machine with sub-parts .  

Now what is a device ? 

A machine is an object with Input Process Output cycle.

But we practically call a machine as a device when it reduce human effort. 

Whatever, Universe if full of machines . The sun , moon , gas to Living being all are ruled by some laws on some measurable properties. 

The Nature follows some rule -

1) Physical Laws are true irrespective of space and time in all Inertial Frames .

2) Uncertainty :- There are pairs of physical quantities where each member of the pair cannot be determined with absolute certainty .

For example : - momentum p(x) and position x . 

                         it is known from  Heisenberg principle that σ(x)σ(p(x))  ≥ h/4π 

Bios + Logos

Now let's satisfy the Biologists :) . But here we will tell some known biological fact with a versatile view.

We are considering  that a subset of Nature is object. So we will classify the subsets of Natures into some classes where each classes follows some property. An object is an instance of each class .

For example Autototropha is  the class of living beings which could make their food . Now a specific rose plant is one instance of Autotroph. A class could have many subclasses (subsets of parent class which are itself a class) and so on.
 
Ok,we already told in previous posts that actions tries to change some property of a body and inertia tries to keep it in that state . More we know that action and reaction occurs between every pair of bodies and that is the only cause of dynamic Universe .
Now let's start observe an object say a small stone . We will see that that tiny object also changing w.r.t to time because in meantime it is interacting with its neighbours.

Now the gradual change of a specific object over a time leads it to enter in a different class that the gradual change in the flow of time changes it so that the object could not be count in its previous class but in a different class.

This is called evolution of an object.

Now obviously the living beings also faced the evolution. Here the evolution is the transformation of a species into another species . A species is actually a class.

Now the evolution is done according to Darwinism in these process :-

1) Every species has to face every time "Struggle of Existence" to sustain .
2) Every living being of a species have gradual changes due to mutation, recombination of properties and selection of better property. So the members of species changes gradually w.r.t time .
3) Nature give more facility to the fitter living being.

When the change become so much that some member of originally one species could not further been told a member of that species then they will enter in one or more new species.

Obviously the changes or metamorphosis does not happen in only the Life but also in every object . There the objects changes from one form to another.

This is the dynamic Universe.

Space-Time Did you Hear That ?

Space-Time this term had been highly popularized from the time of Albert Einstein. Actually we can tell that space could be view as a 3-D vector space on real field (well quite a height mathematical term suppose but you can think that space is a 3-D space). While time is also another dimension with 3 dimensions of space and the combination of these 4 dimension actually give us a vector space which is a 4-D vector space on real field and called the 'Space-Time' . One little thing I want to mention that Einstein was not founder of this term Space-Time . Actually this concept of 4-D came to knowledge just when we introduce the concept of dimensions and understood that space is 3-D and time is another continuous (i.e real) dimension (because now we can choose time as another dimension).

Def(Space-Time) :- It is a 4-D vector space over real field having 3 distance and 1 time dimension and a point in space-time is called an event.

 

Physical Laws

Let's discuss about a specific core physical view -
Some facts about the Nature :-
Def (Object):- An object is a subset of nature .
Def (Action):- An action is something which changes/ tries to change (viz. shape, structure etc.) some property of an object with respect to time.
Action always be done by some object(actor) on other object(reactor),on which the changes will occur.
Actually the change with respect to time give us the concept of dynamic Universe ( i.e Universe that changes w.r.t time ). More the change is main cause behind that we can feel that something like time exists :).

1) Property of Interaction :-  'Every atomic (not divisible into parts) objects in nature interacts with each of other objects in nature.' 
If an object has parts i.e if it could be further fragmented into smaller atomic parts then according to the above theorem each of those atomic parts interacts with other parts of that non-atomic object as well as objects outside that non-atomic object in which they reside.

2) Acton Reaction pair only exist :- 'Action always happens only with equal and opposite reaction where reaction taken place in body which did the action(i.e by reactor on actor), also actions are only mutual (i.e only interactions exist).'

4) Existence of Inertia :- 'Every object has an tendency (called inertia) to apply a repulsion to the incoming action.'

For this reason if you hit a standalone ball the ball tries to sustain in its state of 0 velocity according to the mass (the amount of physical inertia against force) the velocity increases.

These laws were well observed and formularised by Sir Issac Newton . :) 

Nature

What is Nature?
Ans. " Nature is the collection of everything which exist. "
Human, other animals, trees, other living objects, dead objects are all parts of Nature.

There are many view to see/describe the Nature. Actually whatever we sense or imagine are all parts of Nature.
[ Suppose you saw in your dream that somewhere trees are growing in the sky. One can ask that whether it is a Natural phenomenon. The answer is simple the dream (i.e a collection of image and sensation from subconscious mind) is itself a Natural phenomenon and the ' trees growing in the sky ' I did not see such incident in daylight without narcotics at least :) ]